Die Zunahme an nachgewiesenen Coronafällen ist keine Folge häufigerer Tests

Die aktuell starke Zunahme von Corona-Neuinfektionen wird wieder eine Debatte über die Aussagekraft der Zahlen auslösen. Doch klar ist, die Zunahme an nachgewiesenen Infektionsfällen ist keine Folge zunehmender Testzahlen oder gestiegener Testkapazitäten. Eine statistische Ausarbeitung für Zweifler.

Eine der häufigsten Aussagen, die sich in den vergangenen Wochen über die zunehmenden Infektionszahlen in Diskussionen findet, ist dass diese Folge zunehmender Testzahlen sein. Es erscheint einladend, einfach prozentuale Anteile zu errechnen (bspw. 2% aller Tests sind positiv) und daraus herzuleiten, dass für jede beliebige Menge an Tests immer 2% Positivfälle folgen müssen. Die Annahme ist einfach und einfach falsch. Die richtige These wäre: Besteht zwischen der Zunahme/Abnahme an Tests ein direkter, linearer und nachweisbarer Zusammenhang zur Zunahme/Abnahme der positiven Fallquoten.

Basierend auf dieser fehlerhaften Annahme wird ein Konstrukt verschiedener Theorien und Vermutungen aufgebaut, die häufig Zweifel an der politischen Intention der deutschen Regierung wecken sollen. Anhand des pyramidalen Prinzips wird argumentativ dargelegt, dass sämtliche, derartige Thesen nachweislich falsch sind. Hierzu wird sich der OLS Regression bedient, einer Methode aus der Statistik. Der vorliegende Artikel ist sehr ausführlich und dem Bestreben geschuldet, das Vorgehen in jedem Schritt so kleinteilig zu erklären, dass die Methodik und nachfolgend meine Ergebnisse nachvollziehbar sind, auch ohne statistische Vorkenntnisse.

Die Schlussfolgerungen finden sich in Abschnitt 1), die mathematischen Ergebnisse und Regressionsbeschreibungen in Abschnitt 2, die Erklärung und Beschreibung der Methodik in Abschnitt 3). Merken Sie sich bitte zwei Werte: t-Statistik über 2,064, p-Wert unter 0,05.

Um das kurz vorweg zu nehmen: Die angewandte Methodik ist weltweit im Einsatz. Es ist kein „man muss die Statistik nur richtig lesen“ oder „traue keiner Statistik, die du nicht selbst gefälscht hast“. Es ist mathematische Methodik, die zweifelsfrei belegt und bei der Beschreibung linearer Zusammenhänge wissenschaftlicher Goldstandard ist.

Der Datensatzes basiert ausnahmslos auf Zahlen von statista (1,2), die Statistiken sind frei zugänglich, die Quellen sind benannt. Alle Berechnungen folgen aus den öffentlich einsehbaren Datentabellen.

1. „So what?“ Schlussfolgerungen und Zusammenfassung der Ergebnisse

Die Lieblingsfrage meines Professors nach jeder Regression war immer „So what?“

Zunächst inhaltlich. Anhand einfacher, linearer OLS Regressionen und statistischer Datensätze wurden unterschiedliche Thesen untersucht, die bis auf einen Sonderfall vollständig widerlegt werden konnten. Es lässt sich klar belegen, dass kein Zusammenhang zwischen der Zunahme an Tests und der Zunahme an positiven Testergebnissen besteht. Ebenfalls besteht keinerlei Zusammenhang zwischen der Zunahme an Testkapazitäten und der Zunahme an Tests. Eine Reihe weiterer Regressionen stützt die Aussagen ausnahmslos. Die Ergebnisse sind statistisch unzweifelhaft und robust für jedes relevante Signifikanzniveau (bedeutet: die Wahrscheinlichkeit eines Irrtums ist quasi 0). Hierzu wurden nur offizielle Zahlen genutzt, die frei und für jedermann verfügbar sind.

Die wichtigsten inhaltlichen Schlussfolgerungen sind:

• Die relevanteste Größe ist die Anzahl an Verdachtsfällen (1), die zur Testung geschickt werden (Testgesamtheit). Die Anzahl an Verdachtsfalltestungen steht in keinerlei Zusammenhang mit den Testkapazitäten (Abs. 2, Thesen 1&2). Es wäre, stand heute, möglich noch deutlich mehr Menschen zu testen (Abs. 2, These 1). Eine logische Schlussfolgerung ist daher, dass Gesundheitsämter und Ärzte einem logischen Prozedere bei der Testung folgen und Risiken schlüssig bewerten.
• Die Anzahl an Coronatests erklärt höchstens zu 16% die Zunahme an positiven Coronatests. Dies jedoch auch nur, wenn die Entwicklung seit KW15 betrachtet wird. Seit KW27 ist ein solcher Zusammenhang nicht nachweisbar (Abs. 2, These 2).
• Die Zunahme der Positivquote belegt, dass es zu einer stärkeren Verbreitung des Coronavirus kommt. Dies ist unzweifelhaft. Die Zunahme an positiven Fallzunahmen lag in den vergangenen Wochen bei im Schnitt über 13%, die Zunahme an absoluten Fallzahlen ist exponentiell (Abs. 2, These 3.1).
• Die Anzahl an Tests sowie die Zunahme an positiven Testergebnissen ist nicht fremdgesteuert, eine Beeinflussung findet nicht statt. Wäre dies der Fall, müssten eine massive Zunahme an absoluten Tests sowie eine Abnahme der Positivquote zu beobachten sein. Das Gegenteil ist der Fall. Die Anzahl an Coronatests ist seit sechs Wochen nahezu konstant, wobei die Zunahme an Testkapazitäten deutlich rückläufig ist. Es kommt nicht zu einer massiven Zunahme an Tests, zeitgleich steigt die Quote positiver Fälle an der Testgesamtheit (Abs. 2, These 3.2).
• Besonders besorgniserregend wäre es, wenn sich der Trend der positiven Fallquotenentwicklung fortsetzt. Mit Beginn der Grippesaison werden zahlreiche Patienten in die Praxen strömen, deren Symptome nicht klar der Grippe oder dem Coronavirus zugeordnet werden können. Es wäre für die Zukunft zu erwarten, dass die Positivquote rückgängig ist, da Grippepatienten ein negatives Testergebnis erhielten.

2. Gefühlte Wahrheiten – Regressionsanalysen und Ergebnisse

Zunächst ist es richtig, dass die Anzahl an positiven Tests auch aus der Anzahl an Tests selbst folgt. Nur, wenn überhaupt getestet wird, kann es auch positive Testergebnisse geben. Keine Tests – keine positiven Tests. Kolportiert wird nun aber, dass es in den vergangenen Wochen, insbesondere seit den Sommerferien, zu einer erheblichen Zunahme an Tests gekommen sei, die die Zunahme an positive Coronatests begründe. Volkskontrolle, eine faschistoid-diktatorische Kanzlerin, Dämonisierung von Sommerurlaubern, Volksversklavung, Chips von Bill Gates, suchen Sie sich ihre Lieblingserklärung aus. Man hat Kapazitäten aufgebaut, Geld ausgegeben für die böse Pharmalobby und jetzt muss der deutsche Michel die Zeche zahlen – oder?

Um der offensichtlichen Korrelation zwischen Testkapazitäten und Testzahlen (Ohne Kapazitäten – keine Tests – keine positiven Ergebnisse) aus dem Weg zu gehen, werden bei den meisten Schätzungen die prozentualen Veränderungen gegenüber der Vorwoche betrachtet. Bestünde hier ein klarer Zusammenhang, wäre dies ein stichhaltiges Indiz für die These, dass die Coronakrise gefaked wurde.

Sofern relevant, betrachte ich zwei Zeitpunkte. Seit KW15, da hier ein Grundstock an Testkapazitäten aufgebaut war, der eine exakte Zuordnung der Tests und Ergebnisse zur Kalenderwoche erlaubt sowie ab KW27, um die These zu be- oder widerlegen, dass es seit den Sommerferien zu einer gezielten Beeinflussung der Testergebnisse kam.

These 1: „Zu Beginn der Krise gab es begrenze Kapazitäten, weshalb nicht mehr getestet wurde. Nun gibt es mehr Kapazitäten, weshalb auch mehr getestet wird.“

Die These ist falsch. Die Auslastung der Labore war nie kritisch und steht in keinem Zusammenhang zur Anzahl an Tests.

Das Argument der Corona-Gegner hier ist, dass die Testkapazitäten der Flaschenhals waren. Seit KW 13 (März) lag die Kapazitätsauslastung nie bei über 79,79%, im Mittel lag sie bei 50,53%. Besonders auffällig ist, dass die Laborauslastung über die vergangenen sechs Wochen rückläufig war (2). Gingen wir in der Annahme, es sei das Bestreben der Regierung Merkel, möglichst viele Coronafälle zu generieren, dann wäre es ausgesprochen kontraproduktiv, Kapazitäten nicht zu nutzen.

These 2: Die Zunahme an Testkapazitäten führt zu einer Zunahme an Tests!

Die These ist falsch. Die Zunahme/Abnahme an Tests steht in keinem Zusammenhang zu den Testkapazitäten.

Hierbei handelt es sich um die eigentlich relevante These. Sie könnte, so sie wahr wäre, das zentrale Argument der Corona-Gegner stützen, dass die Testanzahl quasi extern vorgegeben wird. Mal angenommen, es würden absichtlich Kapazitäten aufgebaut, um möglichst viel zu testen, Infizierte zu finden und somit den Druck auf die Bevölkerung zu erhöhen, dann müsste sich aus der Steigerung an Testkapazitäten ganz klar eine Steigerung der Coronatests herleiten lassen.

Die Testkapazität wurde gesteigert und hat sich seit KW 13 ungefähr verdreifacht. Zur Klärung der These muss nun die Zunahme/Abnahme der Kapazitäten und Testzahlen betrachtet werden. In den ersten Wochen kam es zu einem regelrecht panischen Aufbau an Testkapazitäten, der für die, auf die aktuelle Entwicklung bezogenen Ausgangsthese, nicht relevant ist. Entsprechend betrachte ich einmal die Regression ab KW15, da es ab KW15 nicht mehr zu Kapazitätssteigerungen im dreistelligen Bereich kam, die jede Schätzung verzerren sowie die Zahlen ab KW27, eine Woche nach Beginn der Sommerferien. Anhand der Regression zeigt sich, dass die Veränderung der Testkapazitäten lediglich 2,1% der zu beobachtenden Varianz erklären. Die t-Statistik ist negativ und liegt deutlich unterhalb jedes kritischen Wertes (dieser müsste über 2,064 liegen), der p-Wert hingegen weit oberhalb jedes relevanten Wertes (dieser müsste unter 0,05 liegen).

Betrachten wir die Zahlen ab KW 27, so zeigt sich ein noch aussagekräftigeres Bild. Lediglich 0,0058% der zu beobachtenden Varianz werden von der Regression erklärt. t-Statistik und P-Wert belegen klar, dass die Veränderung der Testkapazitäten keinerlei erklärenden Einfluss auf die Veränderung der Testzahlen hat.

Nun ließe sich argumentieren, dass die Zunahme an Testkapazitäten erst in der folgenden Woche zu einer Zunahme an Tests führt (Adaptionszeit). Die Regression KW15V berücksichtigt diese Verschiebung. Die Anpassung des Fits ist mit 8,9% der auftretenden Varianz besser, t-Statistik und P-Wert belegen jedoch weiterhin, dass kein erklärender Zusammenhang für jeden sinnvolle Signifikanzniveau gegeben ist.

Die Aussage, dass die Veränderung der Testkapazitäten erklärenden Einfluss auf die Anzahl an Tests hat, lässt sich zweifelsfrei widerlegen. Dies ist auch logisch, da die Testkapazitäten niemals der limitierende Faktor waren.

These 3: Die Zunahme an Tests ist die (alleinige) Ursache für die Zunahme an positiven Ergebnissen

Die These ist größtenteils falsch. Die Zunahme an Tests erklärt nicht die Zunahme an positiven Ergebnissen.

Zur Klärung der These müssen zwei Subthesen behandelt werden:

• Eine Zunahme an Tests führt zu einer Zunahme an positiven Fällen

Hier muss man nun diskutieren, wer und weshalb getestet wird. Nehmen wir einmal an, jede Woche würden eine Millionen Deutsche quasi auf Befehl der Kanzlerin persönlich zum Test gezwungen, dann wäre eine völlige Zufallsverteilung gegeben. Ließe sich nun herleiten, dass ein direkter, linearer nicht zwingend proportionaler Zusammenhang bestünde, dann wäre die Angelegenheit ganz klar: Das Coronavirus ist völlig willkürlich verteilt, je mehr getestet wird, desto mehr steigen die Infektionszahlen.

Es wird aber nicht willkürlich getestet. Tests erfolgen nur im begründeten Verdachtsfall, konkret bei Kontakt ersten Grades mit einer Person, die nachweislich mit dem Coronavirus infiziert ist oder aber bei symptomatischen Patienten, deren Symptome eine Infektion mit dem Coronavirus wenigstens wahrscheinlich erscheinen lassen.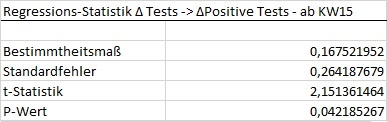

Größtenteils (und vermutlich vollständig) falsch deshalb, weil ein Zusammenhang grundsätzlich besteht. Bei einer t-Statistik von 2,15 (dieser müsste über 2,064 liegen) und einem P-Wert von 0,04 (dieser müsste unter 0,05 liegen) ist ein erklärender Anteil der Zunahme an Tests an der Zunahme positiver Fälle gegeben. Die Irrtumswahrscheinlichkeit ist, angesichts der starken Annäherung an die kritischen t- und P-Werte, jedoch ausgesprochen hoch und liegt bei wenigstens 5%. Weiterhin werden lediglich 16% der Varianz (Bestimmtheitsmaß) erklärt, das ist sehr wenig. Anders (und stark vereinfacht) ausgedrückt: Wenigstens 84% der prozentualen Veränderung der positiven Fallzunahmen sind nicht durch die prozentuale Zunahme an Tests zu erklären.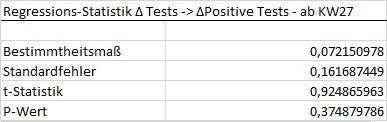

Die Annahme, dass die These vermutlich gänzlich falsch ist, stützt die Regression der Zahlen ab KW27. Hier liegt das Bestimmtheitsmaß bei lediglich 7,2%, die niedrige t-Statistik sowie der zu hohe P-Wert legen nahe, dass die Nullhypothese nicht verworfen werden kann, sprich kein erklärender Einfluss der Zunahme an Tests auf die Zunahme an positiven Tests gegeben ist.

• Es wird einfach so lange getestet, bis man die notwendige Anzahl positiver Fälle zusammen hat

Nehmen wir einmal an, die Regierung wolle zwingend eine Steigerung der Infektionszahlen belegen. Nachdem Gesundheitsminister Spahn in diktatorischem Eifer den Befehl gegeben hat, werden Menschen zum Test genötigt, bis endlich genügend Menschen positiv getestet wurden. Wäre dies so, dann müsste der Anteil positiver Tests an der Gesamtheit an Tests logischerweise abnehmen. Es müsste ein negativer Zusammenhang zwischen der Zunahme an Tests und dem Anteil positiver Tests bestehen, weiterhin müsste es zu einer erheblichen Zunahme an Testzahlen kommen.

Zunächst zur Veränderung der Testzahlen. Gemittelt werden seit KW27 7,54% mehr Menschen getestet, als in der Vorwoche. Gemittelt seit KW15 sind es sogar nur 4,96%. Widersprüchlich zur These ist hier, dass sich in den vergangenen Wochen ein klar rückläufiger Trend erkennen lässt. Die prozentuale Zunahme an Tests ist, gegenüber der Vorwoche, zuletzt stark zurückgegangen. Behalten Sie im Kopf, dass die Testkapazitäten lange nicht ausgenutzt werden. Es wären wesentlich mehr Tests möglich.

Die Regressions-Statistik belegt, dass kein Zusammenhang zwischen der Zunahme an Tests und dem Anteil positiver Tests an der Testgesamtheit besteht. Konkret ist es so, dass der Anteil positiver Tests seit KW27 im Mittel um 4,5% zugenommen hat. Die Zahlen belegen unzweifelhaft, dass ganz offenbar ein Effekt vorliegt, der dafür sorgt, dass die prozentuale Veränderung positiver Tests zunimmt. Die logischste Erklärung hierfür lautet: Es infizieren sich einfach deutlich mehr Menschen mit dem Virus.

3. Methodisches Vorgehen

OLS Methodik

Die OLS (Ordinary least squares) Regression, zu Deutsch Methode der kleinsten Quadrate bestimmt anhand einer Anzahl an Datenpunkten eine Funktion, deren Verlauf für alle betrachteten Punkte eine möglichst exakte Durchschnittsannäherung beschreibt. Hierbei wird eine Anzahl an Parametern bestimmt, die Aussagen über den statistischen Zusammenhang zulassen. Wir sprechen hierbei von der abhängigen Variablen und der unabhängigen Variablen.

Die zwei Grafiken unten verdeutlicht den Zusammenhang. Die sich stellende Frage lautet: Lässt sich anhand des X-Wertes (unabhängige Variable) der Y-Wert (abhängige Variable) vorhersagen? Gibt es eine Funktion, die den Durchschnitt der zu beobachtenden Ergebnisse möglichst gut beschreibt?

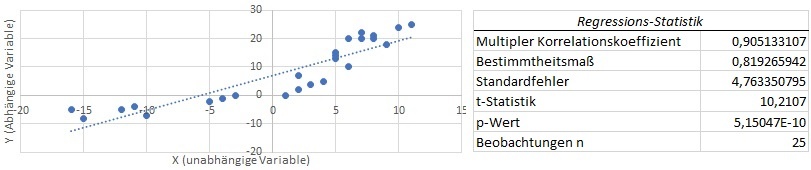
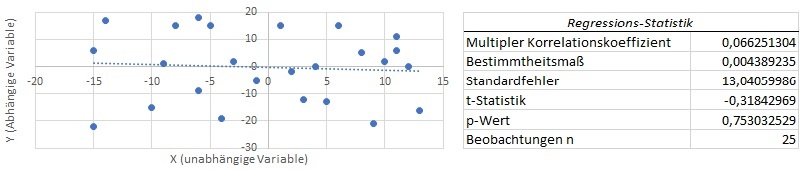
In der Grafik 1 lässt bereits die blaue Trendlinie den Schluss zu, dass ein solcher Zusammenhang offenbar gegeben ist und das beobachtete Y der Datenreihe anhand des X-Wertes prognostizierbar ist. In Grafik 2 ist ein solcher Zusammenhang sehr unwahrscheinlich.

Nun kommen wir zur Teststatistik. Hierbei sind drei Werte von besonderer Bedeutung, der r², der t-Wert und der p-Wert.

Bestimmtheitsmaß r²

Der r² ist das Bestimmtheitsmaß. Vereinfacht ausgedrückt gibt das Bestimmtheitsmaß an, wie genau die errechnete Funktion und die hieraus folgende Trendlinie die Datenpunkte „vorhersagt“. Je näher der r² an 1 ist, desto besser sind das Modell und die Prognose.

t-Statistik, p-Wert und Nullhypothese

Bei der OLS Regression werden zwei Annahmen gegeneinander bewertet. Die Annahme, dass ein linearer (nicht zwingend proportionaler) Zusammenhang zwischen der unabhängigen Variablen und der abhängigen Variablen besteht gegenüber der Nullhypothese, der Annahme, dass zwischen der erklärenden (unabhängigen) Variablen und der abhängigen Variablen kein Zusammenhang besteht, sprich der Zusammenhang „vermutlich“ null ist. Eine von beiden Annahmen muss verworfen werden.

Ob die Nullhypothese verworfen werden kann (der Parameter also relevant für Schätzung ist), lässt sich anhand der t-Statistik und des p-Wertes feststellen. Ohne zu tief methodisch einzusteigen: Zur Bewertung der t-Statistik wird die standardisierte t-Verteilungstabelle herangezogen, die abhängig von der Anzahl an Freiheitsgraden (das ist die Anzahl der Beobachtungen abzüglich der Anzahl geschätzter Parameter) und unterschiedlicher Signifikanzniveaus kritische t-Werte benennt. Kritisch deshalb, weil eine t-Statistik wenigstens gleich oder großer des hier benannten Werts bedeutet, dass der Parameter, in diesem Beispiel X, zum gewählten Signifikanzniveau relevant für die Schätzung von Y ist. Also: X erklärt Y und das nicht rein zufällig, sondern kausal.

Das Signifikanzniveau lässt sich umschreiben als Irrtumswahrscheinlichkeit. Bei einem Signifikanzniveau von 95% bedeutet dies, dass mit einer Wahrscheinlichkeit von 5% fälschlicherweise die Nullhypothese abgelehnt wird, ergo: Fälschlicherweise davon ausgegangen wird, dass X signifikant für die Erklärung von Y ist. Ebenfalls ablehnen lässt sich die Nullhypothese, wenn der p-Wert kleiner ist als das gewählte Signifikanzniveau, angegeben in 1/100. Nehmen wir als Beispiel ein Signifikanzniveau von 5%. Wir haben 25 Beobachtungen (n=25) und einen geschätzten Parameter. Folglich ergeben sich 24 Freiheitsgrade.

Aus der t-Verteilungstabelle folgt hierfür ein Wert von 2,064 (3).

Bei einem zweiseitigen Test errechnet sich der relevante Wert als 1 – (Signifikanzniveau/2). Sofern die t-Statistik also größer oder wenigstens gleich 2,064 und der p-Wert kleiner 0,05 ist, lässt sich die Nullhypothese verwerfen.

Beispielstatistiken

Betrachten Sie nun die Regressions-Statistiken, die zu den beiden vorstehenden Grafiken gehören.

Für Grafik 1 ist ein klarer, linearen Zusammenhang mit einer mathematischen Anpassung des Modells von 0,819 ersichtlich (sachlich korrekt: 81,9% der beobachteten Varianz werden vom Modell erklärt), die t-Statistik von 10,21 ist deutlich größer als 2,064, der p-Wert deutlich kleiner als 0,05 (5.15047E-10 ist die wissenschaftliche Schreibweise von 0.000000000515047). Sprich: Die erklärende Variable X liefert einen signifikanten Erklärungsanteil an unserer Beobachtung Y.

Bei Grafik 2 ist ein linearer Zusammenhang nicht zu erkennen. Die Anpassung von 0,004 (4% der Varianz werden vom Modell erklärt) ist ausgesprochen gering, die t-Statistik ist negativ (und somit deutlich kleiner als 2,064), der p-Wert größer als der kritische p-Wert von 0,05. Sprich: Die Nullhypothese lässt sich nicht verwerfen, mit größtmöglicher Wahrscheinlichkeit liefert X keinen Erklärungsanteil für die abhängige Variable Y.

Datenqualität

In meiner Abschlussarbeit an der TU Dortmund habe ich in den Empirie-Teil meiner Arbeit mit dem Abschnitt „Das Problem von Datenanalysen sind die Daten“ begonnen. In der Informatik kennt man die Floskel „Garbage in – Garbage out“. Nur, wenn Daten sinnvoll gewählt sind, kann auch ein sinnvoller Zusammenhang konstruiert werden. Entsprechend muss zunächst überlegt werden, welche Datenreihe geeignet ist, um zu analysieren, ob sie eine andere Datenreihe erklären kann.

Das Problem sind Korrelationen und Kausalitäten. Eine Kausalität ist gegeben, wenn aus einer Zahl/Handlung/etc. A klar ein Ergebnis/Folge/etc. B resultiert. Eine Korrelation hingegen, wenn A und B scheinbar zusammenhängen, ohne, dass A B oder B A erklärt.

Wenn Sie ab morgen ihre Kalorienaufnahme (ohne weitere Änderungen an Lebensgewohnheiten) um 3.000 pro Tag steigern, dann werden Sie zunehmen. Das ist eine klare Kausalität. Essen -> Gewicht. Scheinkorrelationen hingegen erfreuen sich in der Wissenschaft als Gag großer Beliebtheit. Ein Zusammenhang besteht aber nicht, es ist reiner Zufall.

Viele, anschauliche und ausgesprochen witzige Beispiele zu Scheinkorrelationen finden Sie unter https://scheinkorrelation.jimdofree.com.

Schlussbemerkung

Die von Verschwörungstheoretikern und Coronaleugnern konstruierten Zusammenhänge basieren auf statistischer Unkenntnis und Fehlannahmen. Der vorliegende Artikel dient nicht dazu, den Umfang der Maßnahmen in gut oder schlecht einzuteilen. Er soll lediglich belegen, dass die von vielen Bürgerinnen und Bürgern gefühlten Zusammenhänge nicht bestehen.

Sollten Sie bis hierhin gelesen haben, möchte ich mich persönlich bedanken und eine Warnung mitgeben. Wenn Sie jetzt noch behaupten, es gäbe einen Zusammenhang zwischen den Testzahlen und den Fallzahlen, dann irren Sie nicht mehr, dann lügen Sie mit Vorsatz.

Quellen:

1. https://de.statista.com/statistik/daten/studie/1107749/umfrage/labortest-fuer-das-coronavirus-covid-19-in-deutschland/
2. https://de.statista.com/statistik/daten/studie/1110951/umfrage/testkapazitaeten-fuer-das-coronavirus-covid-19-in-deutschland/
3. http://eswf.uni-koeln.de/glossar/tvert.htm
4. Datensatz – D. Bleich – Ruhrbarone

Alle Grafiken und Regressions-Statistiken wurden von mir erstellt. Diese dürfen, unter Quellenverweis, gerne genutzt werden.